Общие начала математики
При всем своеобразии развития математических приемов у разных народов общее для них всех в том, что основные понятия: числа, фигуры, площади, бесконечно продолжающийся натуральный ряд и так далее, возникли из практики. Например, понятие числа понадобилось для пересчета предметов. Вначале счет производился с помощью подручных средств: пальцев, камней и т. д. Так, латинское calculus означает счет камешками.
Запас чисел на ранних ступенях был весьма ограничен, он удлинялся лишь постепенно. А с употреблением все больших и больших чисел возникали и развивались их символы, а сами числа образовывали системы.
В каждой из иероглифических непозиционных систем счисления строится система так называемых узловых чисел (чаще всего 1, 10, 100, 1000,…). Каждое такое число имеет индивидуальный символ – иероглиф. Остальные числа (их называют алгоритмическими) образуются приписыванием с той или другой стороны узлового числа других узловых чисел и повторением их. Так, система чисел, ныне известная как римская, имеет систему узловых чисел: I, V, X, L, С, D, М. Ее происхождение неизвестно. Построена по десятичному признаку с заметным влиянием пятеричной системы, а между тем в латинском языке никаких следов пятеричной системы нет, значит, цифры заимствованы римлянами у другого народа.
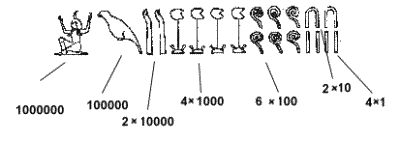

Основные цифровые знаки Египта и что они обозначают иероглифически
Выполнять арифметические действия над многозначными числами в этой записи очень трудно. Тем не менее римская нумерация преобладала в Италии до XIII, а в других странах Западной Европы – до XVI века.
К иероглифической системе относятся и алфавитные системы счисления. В них буквы алфавита, взятые группами по 9, используются соответственно для обозначения единиц, десятков и сотен. Каждой букве при этом дается отличительный знак (титл, черточки над цифрами), указывающий, что буква используется как число. Если букв алфавита было недостаточно, привлекали дополнительные знаки. Типичный пример алфавитной системы – византийская, арабская, славянская. А это и понятно: они вышли из одного источника.
Историки науки считают, что в древнейшее время в Греции применялась так называемая аттическая нумерация, при которой числа 1, 2, 3, 4 обозначались черточками | || ||| ||||. Число 5 записывалось знаком П (древнее начертание буквы «пи», с которой начинается слово «пенте» – пять); числа 6, 7, 8, 9 обозначались П|, П||, П|||, П||||. Число 10 обозначалось Д (начальной буквой слова «дека» – десять). Числа 100, 1000 и 10 000 обозначались Н, X, М – начальными буквами соответствующих слов. Числа 50, 500, 5000 обозначались комбинациями знаков 5 и 10, 5 и 100, 5 и 1000.
Эта система очень напоминает римскую, ведь и числа римского счета I, V, X, L, С, D, М одновременно были буквами, и к ним тоже добавляются «палочки». Причем римская система применялась в Европе до перехода на так называемые арабские, а на самом деле индийские цифры, имевшие почти современный вид; Византия перешла на них в XII веке, на 200 лет раньше Западной Европы. Можно предположить, что аттическая нумерация была навязана грекам Византии латинянами, после захвата ими Царьграда и Греции в ходе 4-го Крестового похода 1204 года.
После аттической нумерации греки якобы выбрали другую, ионийскую систему – полагают историки. В ней числа от 1 до 9 обозначаются первыми девятью буквами алфавита. Числа 10, 20, 30,…, 90 – следующими девятью буквами. Числа 100, 200,…, 900 – последними девятью буквами. А мы напомним, что эту систему в IX веке позаимствовали из Византии славяне, так что в Византии она могла быть не позже, а раньше аттической.
Преимущество алфавитных систем в краткости записи, однако они мало пригодны для оперирования с большими числами и требуют значительных усилий для запоминания.
Со временем сформировались позиционные недесятичные, а затем десятичная системы. К позиционным недесятичным системам относится вавилонская, к позиционной десятичной – индийская. О них мы поговорим чуть позже.
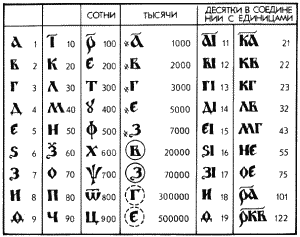
Славянские цифры
Люди в разных местах и в разное время постепенно накапливали эмпирические знания, развивая ремесло, земледелие, обмен и торговлю. Эти знания подвергались систематизации; так выделился особый вид понятий и методов решения задач. Пересчет элементов конечных множеств, а также упорядочивание этих элементов привели к понятию натурального числа, как количественного, так и порядкового. Сравнение масс предметов, объемов сосудов, расстояний дали понятие величины. Изучение формы изделий, зданий, земельных участков вывело к понятию геометрической фигуры, как части геометрического пространства (само слово геометрия в переводе с греческого означает «землемерие»).
Так же из повседневной практической деятельности сформировались и другие математические понятия: площади, объема и прочих абстракций пространственных свойств предметов.
Ведь создание математической науки есть прежде всего переход к абстракциям. Вместо счета стрел, голов скота и т. д. родилось абстрактное понятие числа. Стало возможным предварять непосредственное оперирование с вещами оперированием с их упрощенными, схематическими изображениями и наименованиями (символами).
Наконец, наступил период, когда это знание стало востребованным в заметных масштабах, в обществе образовалась прослойка людей, умеющих пользоваться совокупностью математических приемов. С этого момента, можно сказать, начала существовать математика как наука.
Прежде всего началась арифметика. Предмет ее составляют не числа, а система чисел с ее связями и законами, да и сама арифметика может быть определена как наука об отношениях между числами. Само же слово арифметика происходит от греческого «искусство счета» (арифмос – число и техне – искусство). Что касается слова математика, то от греческого mathema – значение, наука, знание. С толкованием определения математики и сегодня не все достаточно ясно. Довольно сильной является традиция ее трактовки не столько как науки, сколько как языка науки.
