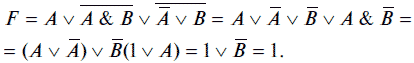Основные законы алгебры логики и правила преобразования логических выражений
В алгебре логики имеются законы, которые записываются в виде соотношений. Логические законы позволяют производить равносильные (эквивалентные) преобразования логических выражений. Преобразования называются равносильными, если истинные значения исходной и полученной после преобразования логической функции совпадают при любых значениях входящих в них логических переменных.
Для простоты записи приведем основные законы алгебры логики для двух логических переменных А и В. Эти законы распространяются и на другие логические переменные.
1. Закон противоречия:
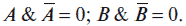
2. Закон исключенного третьего:
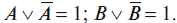
3. Закон двойного отрицания:
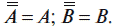
4. Законы де Моргана:
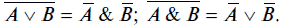
5. Законы повторения: A & A = A; A v A = A; В & В = В; В v В = В.
6. Законы поглощения: A ? (A & B) = A; A & (A ? B) = A.
7. Законы исключения констант: A ? 1 = 1; A ? 0 = A; A & 1 = A; A & 0 = 0; B ? 1 = 1; B ? 0 = B; B & 1 = B; B & 0 = 0.
8. Законы склеивания:
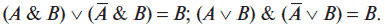
9. Закон контрапозиции: (A ? B) = (B ? A).
Для логических переменных справедливы и общематематические законы. Для простоты записи приведем общематематические законы для трех логических переменных A, В и С:
1. Коммутативный закон: A & B = B & A; A ? B = B ? A.
2. Ассоциативный закон: A & (B & C) = (A & B) & C; A ? (B ? C) = (A ? B) ? C.
3. Дистрибутивный закон: A & (B ? C) = (A & B) ? (A & C).
Как уже отмечалось, с помощью законов алгебры логики можно производить равносильные преобразования логических выражений с целью их упрощения. В алгебре логики на основе принятого соглашения установлены следующие правила (приоритеты) для выполнения логических операций: первыми выполняются операции в скобках, затем в следующем порядке: инверсия (отрицание), конъюнкция ( & ), дизъюнкция (v), импликация (?), эквиваленция (?)
Выполним преобразование, например, логической функции
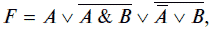
применив соответствующие законы алгебры логики.